KOMPETENZORIENTIERUNG IN DER DISKUSSION: BERLINER ABITUR-NOTEN, ELEMENTARMATHEMATISCHE FÄHIGKEITEN
Angela Schwenk1 und Norbert Kalus2
1 Beuth Hochschule für Technik Berlin, schwenk@beuth-hochschule.de
2 Beuth Hochschule für Technik Berlin, kalus@beuth-hochschule.de
Abstract 1 Eine Auswertung der Abiturdaten in Berlin zeigt für den Zeitraum von 2006 bis 2016 eine deutliche Verbesserung der Abiturergebnisse bezogen auf die Parameter Durchschnittsnote, Anteil der Einsen und Zahl der nicht bestandenen Prüfungen. Dazu gegenläufig sind die Beobachtungen in der Studieneingangsphase. Aus der Perspektive von Ingenieurstudiengängen an einer Fachhochschule werden diese Beobachtungen durch Fallbeispiele demonstriert. Das Besondere an diesen Beispielen ist, dass sie aus Ingenieursfächern kommen und dass bei ihnen mathematisch einfache, praktische Anwendungen im Vordergrund stehen.
Keywords Kompetenzorientierung, Abiturstatistik, Übergang Schule – Hochschule, fehlende elementarmathematische Fähigkeiten
Abstract 2 Over the years from 2006 to 2015 a statistical analysis of the final secondary-school examinations in Berlin reports that the results are enhancing with respect to the parameters average of grades, the portion of best possible grades and the number of failed examinations. But the competencies of first-year students at university have an opposing trend. We will demonstrate these observations from the point of view of engineering study courses at a university of applied sciences and we will give examples. The specific features of these examples are: colleagues of the engineering faculty collected them out of their engineering modules; the focus is on mathematical simple practical applications.
Keywords Competence orientation, statistics of final secondary-school examinations, transition from school to university, lack of mathematical competencies.
Abiturdaten in Berlin der Jahre 2006 bis 2016: Verbesserung aller Parameter
Eine Auswertung der Abiturdaten [KMK] in Berlin zeigt für den Zeitraum von 2006 bis 2016 eine deutliche Verbesserung der Abiturergebnisse bezogen auf die Parameter Durchschnittsnote, Anteil der Einsen und Zahl der nicht bestandenen Prüfungen. Genauer heißt das, die Anzahl der Abiturprüfungen nimmt über die Jahre zu, gleichzeitig sinkt die Zahl der Durchgefallenen, verbessert sich der Notendurchschnitt eines Abiturientenjahrgangs und erhöht sich der Anteil der Prüflinge, die die Bestnote 1,0 erreichen. Diese Entwicklung wird im Folgenden genauer beleuchtet.
Abiturnoten und besondere Veränderungen im Berliner Schulsystem
Wir beginnen mit den Durchschnittsnoten der bestandenen Abiturprüfungen an Gymnasien, Gesamtschulen bzw. integrierten Sekundarschulen und beruflichen Schulen.
In der Abbildung 1 sind die Durchschnittsnoten eines Abiturjahrganges über den Jahren aufgetragen.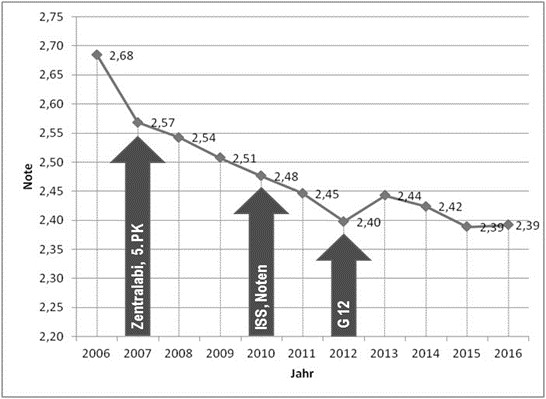 
Dabei beachte man: je niedriger die Kurve ist, desto besser ist die Note. Von 2006 bis 2016 verbessern sich die Noten um ca. 0,3 von 2,68 auf 2,39.
Die Kurve zeigt einige Auffälligkeiten, die sich mit Änderungen im Berliner Schulsystem erklären lassen. Die starke Verbesserung der Noten im Jahr 2007 fällt mit der Einführung der fünften Prüfungskomponente (5. PK) und der Einführung des Zentralabiturs zusammen. Die fünfte Prüfungskomponente besteht aus einer Präsentation über ein selbstgewähltes fachübergreifendes Thema, die seit 2013 durch eine Facharbeit im Umfang von fünf Seiten ergänzt werden muss. Alternativ kann eine schriftliche Belegarbeit angefertigt werden, aber diese Alternative wird kaum gewählt. Die Handreichungen der Berliner Senatsverwaltung für Lehrer zur 5. PK bestätigt die Verbesserung der Noten, dort heißt es gleich im 2. Satz des Vorwortes „In diesem Prüfungsteil erreichen Schülerinnen und Schüler im Durchschnitt bessere Leistungen als in den übrigen Prüfungsfächern.“ [SenBJW, 2012, S. 5] Im Jahr 2013 lag die durchschnittliche Bewertung der 5. PK mit 10,4 Punkten deutlich über den der anderen mündlichen oder schriftlichen Prüfungen mit Durchschnitten von 7,9 bis 8,7 Punkten [Thoren, 2013, S. 42].
Im Jahr 2010 gab es zwei Veränderungen. Zum einen wurden die Integrierten Sekundarschulen (ISS) eingeführt, die die Haupt- und Realschulen in Berlin zusammenführten und die auch zum Abitur führen können. Zum anderen wurde der Notenschlüssel verändert. Die Hürde zum Bestehen wurde von 50% auf 45% der erreichbaren Punkte abgesenkt und der gesamte Notenschlüssel wurde entsprechend angepasst. Die Zeitung Der Tagesspiegel berichtete davon mit der stolzen Überschrift: „Berliner Abiturienten holen bayerische Schüler ein“ [Tgsp, 1.7.2010]. Diese Änderungen führten aber nicht zu einer besonders auffälligen Verbesserung der Abiturdurchschnittsnote des Jahrgangs 2010.
Im Jahr 2012 war der doppelte Abiturientenjahrgang. In Berlin gilt die Verkürzung von 13 auf 12 Schuljahre nur für die Gymnasien. An den IS-Schulen wird das Abitur weiterhin nach 13 Jahren abgelegt. D. h. die stärkeren Gymnasiasten waren im doppelten Abiturientenjahrgang 2012 überproportional vertreten. Im darauffolgenden Jahr 2013 war das Verhältnis wieder normal und dementsprechend sind die Noten von 2013 und 2011 eher vergleichbar.
Verteilung der Noten
Abbildung 2 zeigt die Verteilung der Noten für drei ausgewählte Jahrgänge.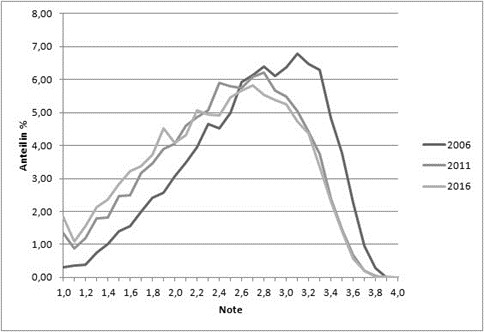 
Die dunkelste Linie gehört zum Abiturjahrgang 2006. Anhand dieser Kurve kann man ablesen, mit welchem Prozentsatz unter allen bestandenen Abiturprüfungen des Jahres 2006 eine bestimmte Gesamtnote erreicht wurde. Die Verteilung entspricht, wie zu erwarten, näherungsweise der Gaußschen Glockenkurve. Die Kurve ist leicht nach rechts zu den schlechten Noten verschoben. Das erklärt sich damit, dass die Grafik nur auf den Daten der bestandenen Abiturprüfungen basiert, also die Noten schlechter als 4,0 nicht erfasst sind. Je heller die Kurve ist, desto neuer sind die Daten. Man erkennt deutlich, dass sich mit den Jahren die Verteilung deutlich nach links, hin zu den besseren Noten, verschiebt. Besonders bemerkenswert ist der Knick bei der Note 1. Schaut man sich die Daten aller Jahre von 2006 bis 2016 im Einzelnen an, dann erkennt man: Ab 2007, dem Jahr der Einführung der 5. PK, ist durchgängig die Häufigkeit der Durchschnittsnote 1.0 höher als die der Durchschnittsnote 1.1. In den Jahren 2009, 2011 (2011 ist ein Jahr nach der Änderung des Notenschlüssels), 2014, 2015 und 2016 ist die Häufigkeit der Durchschnittsnote 1.0 sogar höher als die der Durchschnittsnote 1.2, in 2016 sogar deutlich höher!
In Abbildung 3 zeigt die obere, dunklere Linie den Prozentsatz der nicht bestandenen Abiturprüfungen, dazu gehört die rechte Ordinatenachse. Insgesamt ist die Durchfallquote im betrachteten Zeitraum von 7,5% auf 5% stark zurückgegangen.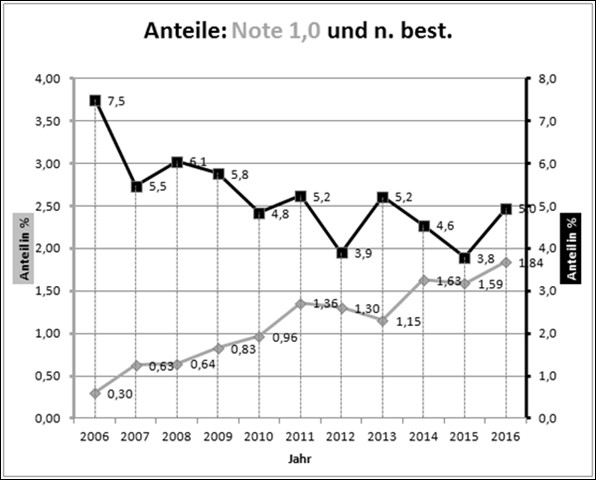 
Im Jahr 2007 der Einführung der 5. Prüfungskomponente und des Zentralabiturs zeigt die Durchfallquote eine besonders starke Verringerung, deutlich ist auch die Verringerung im Jahr 2010, als die Notenskala verändert wurde. Der doppelte Abiturjahrgang 2012 mit der doppelten Kohorte von Gymnasiasten zeigt ebenfalls eine besonders starke Verringerung der Durchfallquote, die im folgenden Jahr 2013 wieder der des Jahres 2011 entspricht.
Parallel zum Rückgang der Durchfallquote hat sich, wie die hellere, untere Linie zeigt, der Anteil der Einser-Abiture, von 0,3% im Jahr 2006 auf 1,8% im Jahr 2016 versechsfacht.
Gegenüberstellung: Anzahl der Prüfungen und der nicht bestandenen Prüfungen
Wie man anhand der Abbildung 3 sehen konnte, verringert sich über die Jahre die Durchfallquote. Aber nicht nur der Prozentsatz der nicht bestandenen Prüfungen nimmt ab, sondern parallel zum Anstieg der Anzahl der Abiturprüfungen nimmt sogar die (absolute) Zahl der nicht bestandenen Prüfungen ab.
In Abbildung 4 sind nun keine Prozentwerte, sondern die absoluten Zahlen dargestellt. Die hellere, obere Linie zeigt mit der linken Ordinatenachse die Anzahl der abgelegten Abiturprüfungen, die schwarze, untere Linie stellt mit der rechten Ordinatenachse den Verlauf der Zahl nicht bestandenen Prüfungen dar.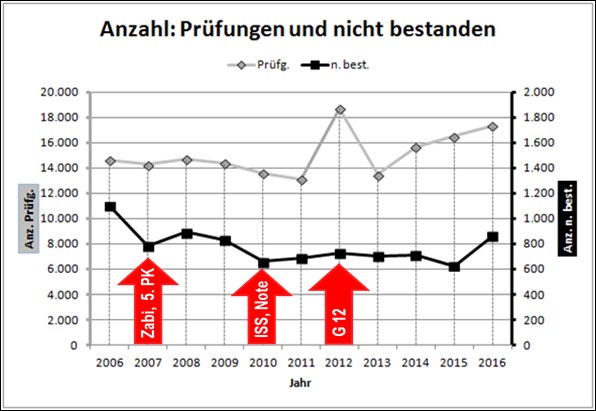 
Deutlich ist der doppelte Abiturientenjahrgang 2012 erkennbar. Ab 2013 steigen dann die Zahlen der Abiturprüfungen deutlich kontinuierlich an. Die Zahl der Durchgefallenen folgt nicht dieser Entwicklung. Mit der Einführung der 5. Prüfungskomponente und des Zentralabiturs in 2007 und mit der Verbesserung der Notenskala in 2010 sinkt die Zahl der Durchgefallenen überproportional. Auffällig ist auch der doppelte Abiturientenjahrgang. Stieg die Zahl der Prüfungen von ca. 13100 (Jahr 2011) um 5.580, das sind 43%, so erhöhte sich parallel dazu die Zahl der Durchfaller nur um ganze 43 Personen, d.h. um 6% und änderte sich kaum. Über den gesamten Zeitraum betrachtet ergibt sich folgendes Bild: 2006 wurden 14650 Abiturprüfungen abgelegt, zehn Jahre später in 2016 waren es 17350; das ist eine Zunahme um 18%. Die Zahl der davon nicht bestandenen Prüfungen ging von 1100 im Jahr 2006 auf 860 im Jahr 2016, d. h. um 22% zurück.
Sinkende Fähigkeiten der Studienanfänger und –anfängerinnen
Konträr zu den guten Entwicklungen der Parameter des Abiturs in Berlin ist die Entwicklung der Fähigkeiten der Studienanfängerinnen und –anfänger. Dies können wir anhand eines Eingangstestes, den wir alle fünf Jahre flächendeckend im ersten Semester an unserer Hochschule durchführen, und weiter unten anhand von Analysen von Fehlern, die in Klausuren beobachtet werden, belegen.
Alle fünf Jahre ermitteln wir die Kenntnisse aller Studienanfänger und –anfängerinnen der Beuth Hochschule für Technik Berlin. Anders als an den Berliner Schulen wurden die Rahmenbedingungen dabei nicht verändert: identische Aufgaben, keine Taschenrechnerbenutzung, anonyme Abgabe, Durchführung in der jeweils ersten Mathematik-Lehrveranstaltung des ersten Semester.
Abbildung 5 zeigt für die Jahre 2000, 2005, 2010 und 2015 die Häufigkeitsverteilung der erreichten Punkte.
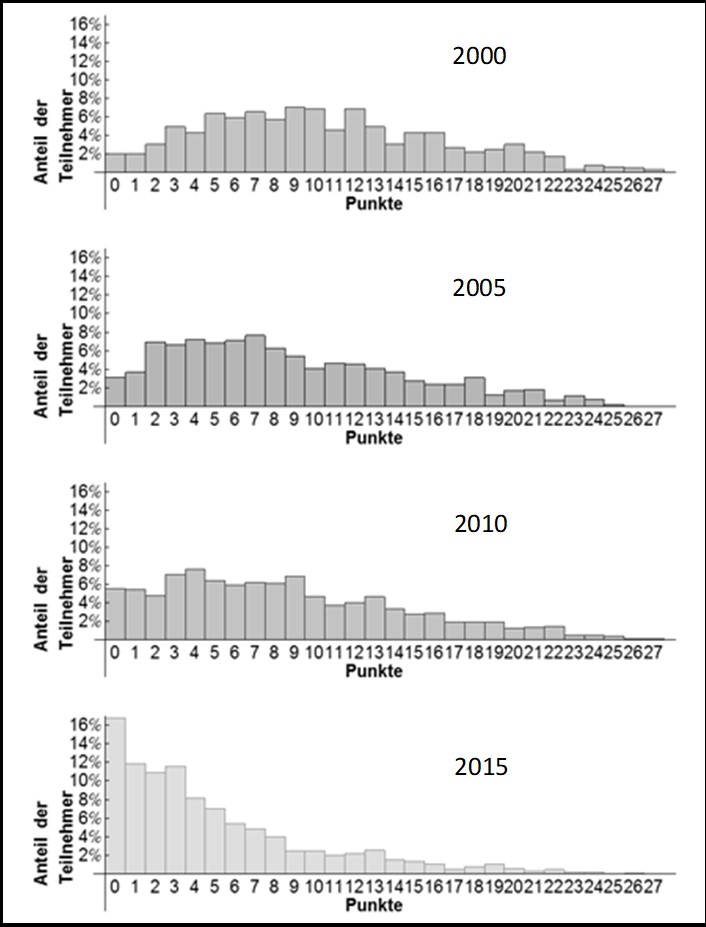Waren es z. B. im Jahr 2000 nur ca. 2 % der Teilnehmer, die keinen einzigen der möglichen 27 Punkte erreichten, so waren es im Jahr 2015 über 16 % aller Teilnehmer. Für die Häufigkeitsverteilungen erwartete man die Form einer Gaußschen Glockenkurve. Eine Glockenkurve ist im Jahr 2000 erkennbar, diese verschiebt sich dann in den folgenden Testjahren immer weiter nach links in den schlechten Bereich. 2015 ist schließlich nur noch die rechte Hälfte der „Glocke” erkennbar.
Parallel haben wir denselben Test in einem Berliner Gymnasium (Bertha-von-Suttner-Schule) u. a. am Ende der 10. Klasse durchgeführt. Damit ist auch klar, dass in dem Test nichts Exotisches verlangt wird, sondern Kenntnisse, die am Ende der 10. Klasse vorhanden sein sollten. Auf die vergleichenden Auswertungen soll hier nicht weiter eingegangen werden.
Der Brandbrief Mathematik und die Reaktionen
Die Hochschulen haben bisher im Allgemeinen den Verfall der mathematischen Eingangskenntnisse nur schweigend beobachtet und sich auf Reparaturmaßnahmen wie die Einführung von Brückenkursen beschränkt. Im März 2017 initiierte Frau Dr. Baumann einen Brandbrief [Baumann, 2017], den 150 Personen aus Universitäten, Fachhochschulen und Schulen unterzeichneten. Inzwischen ist die Zahl der Unterzeichner auf 300 angewachsen. Unterschrieben haben nicht nur Mathematiker/innen sondern auch Ingenieurkollegen/innen. Dieser Brandbrief fand ein breites Echo in den Medien. In sehr vielen Reaktionen auf den Brandbrief wurde auch von Seiten der Mathematik-Didaktik anerkannt, dass es in der Mathematik eine Lücke zwischen Schule und Hochschule gibt. Über die Ursachen herrschte dann keine Einigkeit mehr.
Unterscheidung von allgemeinbildender und studienvorbereitender Mathematik
Nach dem PISA-Schock im Jahr 2000 wurde in Deutschland der Mathematikunterricht an Schulen reformiert. Über die Bildungsstandards hielt die Kompetenzorientierung Einzug in den Schulen. Wissen wurde als totes Wissen bezeichnet, Üben wurde zu Gunsten von Anwendungen, die oft nur pseudo Anwendungen waren, reduziert.
Eigenes Wissen muss strukturiert und vernetzt sein, das ist besonders für die Mathematik wichtig. Dem entgegen steht die Häppchen-Mathematik in Schulbüchern, bei denen auf jeder Doppelseite ein neues Thema begonnen wird [Affolter, 2009]. Die Kompetenzorientierung wurde im Brandbrief als Hauptursache genannt. 50 Didaktiker/innen der Mathematik antworten in einem offenen Brief: „Wie kann ein Mathematikunterricht aussehen, der eine mathematische Allgemeinbildung gewährleistet bei gleichzeitiger Sicherung einer Studierfähigkeit für mathematiknahe Berufe?“. Damit wurde ein Konflikt zwischen allgemeinbildender und studienvorbereitender Mathematik konstruiert. Frau Reiss, die deutsche PISA-Chefin, wurde in der Tagesszeitung Der Tagesspiegel zitiert mit: „Es ist ein fundamentales Missverständnis, dass die Schule die Schüler studierfertig abzuliefern hat.“ [Tgsp, 22.3.2017]. Dieses Zitat macht einen Paradigmenwechsel deutlich. Dazu passt, dass in letzter Zeit immer öfter statt von Hochschulreife von Hochschulzugangsberechtigung gesprochen wird. Auch in der Diskussion in den Nachrichten der Deutschen Mathematiker Vereinigung konstruierten Eichler und Körner [Vogt, 2017] einen Unterschied zwischen mathematischer Allgemeinbildung und der Vorbereitung auf ein MINT-Studium. Unabhängig davon, ob man diese Unterscheidung für gerechtfertigt oder nicht hält, lässt sich festhalten, dass die Probleme im elementarmathematischen Bereich eindeutig in der „allgemeinbildenden Mathematik“ angekommen sind. Dazu folgen ein paar Beispiele.
Beispiele
Die nun folgenden Beispiele gehören eindeutig zur allgemeinbildenden Mathematik. Das besondere dieser Beispiele ist, dass sie alle von Ingenieurkollegen in deren Ingenieur-Modulen gesammelt wurden. Sie stammen also nicht aus dem Elfenbeinturm der Mathematik. Damit ist klar, dass die folgenden Inhalte und Fähigkeiten von den Ingenieurstudierenden „gebraucht“ werden.
Kürzen nicht automatisiert
Aus dem 5. Semester des Bachelor-Studiengangs Maschinenbau stammt diese Aufgabe, sie war ohne Unterlagen und ohne Benutzung eines Taschenrechners im Rahmen einer Klausur zu lösen.
Wie lang ist der Weg, den ein Fräser auf einem Viertelkreis (Durchmesser von 800 mm) zurücklegt?
Es muss also der Umfang eines Viertelkreises bei gegebenen Durchmesser d berechnet werden Die Formel lautet U1/4=π d/4. Nach Einsetzen der Werte und Kürzen muss lediglich das Produkt aus 200*π mm=2*3,14*100 mm=628 mm berechnet werden. Doch ohne Kürzen lauern viele Fallstricke bei der schriftlichen Multiplikation von 800*3,14 mm und dem anschließendem schriftlichen Dividieren durch 4. Dahinter steckt ein typisches Problem: Kürzen vor der Berechnung ist eine kaum noch vorhandene Praxis. Das beobachten wir in unseren Mathematik-Klausuren auch immer wieder. Insgesamt nahmen 67 Studierende an der Klausur teil, 35 von Ihnen bearbeiteten die Aufgabe nicht oder hatten eine falsche Lösung, d. h. 52% der Teilnehmenden erzielten kein korrektes Ergebnis! Viele von denen wussten die korrekte Formel, scheiterten dann wegen des fehlenden Kürzens an der eigentlichen Rechnung.
Umrechnen von Einheiten, Umgang mit Zehnerpotenzen
Nachdem ein Kollege in der Labor-Übung Werkstoffbearbeitung im 1. Semester des Studiengangs Wirtschaftsingenieurwesen Maschinenbau Probleme beim Umrechnen von Einheiten erkannt hatte, ließ er das Thema anhand von Unterlagen üben und erstellte einen Testbogen. Diesen Testbogen benutzte dann einer der Autoren und überprüfte damit unangekündigt die Umrechnungsfähigkeiten bei Studierenden seiner Mathematik I Vorlesung für den Studiengang Maschinenbau.
Die Aufgaben in Abbildung 6 mussten ohne Taschenrechner bearbeitet werden. 
Das Ergebnis war niederschmetternd: Keiner hatte 8 oder alle 9 Aufgaben richtig, und 34% hatten keine oder nur eine Aufgabe richtig. Im Durschnitt wurden von den 9 Aufgaben nur 2,93 richtig gelöst. Dabei verlangen diese Aufgaben nur Basisfähigkeiten: Kenntnisse der Einheitenpräfixe, das Umgehen mit 10er-Potenzen und ggf. elementare Bruchumformungen.
Umformen einer einfachen Gleichung
Dieses Beispiel stammt aus dem Labor für Werkstoffbearbeitung. Dort sollte eine Laborgruppe an der Tafel vor der Versuchsdurchführung die Schnittgeschwindigkeit Vc eines Bohrers berechnen. Die Beziehung zwischen der Umdrehungszahl n des Bohrers pro Minute und dem Durchmesser des Bohrers d war wie in der obersten Zeile von Abbildung 7 gegeben.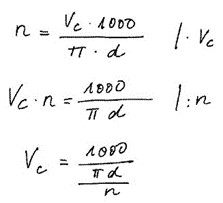 
Die Aufgabe war nun, die Gleichung nach Vc aufzulösen. Ein Student der Gruppe formte um, vier sahen zu, alle fünf hatten Abitur und keiner hat den Fehler gefunden.
Beim Übergang zur letzten Zeile zeigt sich eine weitere Schwierigkeit. Ein Bruch muss hier durch eine Zahl geteilt werden. Offensichtlich war der Student unsicher und notierte erst einmal den Doppelbruch. Das Tafelbeispiel hört hier auf. Wie der Doppelbruch vereinfacht worden wäre, ist also Spekulation. Aber in der Schreibweise zeigt sich ein sehr häufig vorkommendes Problem, das oft zu Fehlern führt, denn die Notation ist nicht eindeutig. Die beiden folgenden Ausdrücke (a/b)/c und a/(b/c) liefern im Allgemeinen verschiedene Ergebnisse. So ist z. B. (2/2)/2=1/2 aber 2/(2/2)=2. Der Bruchstrich außerhalb der Klammer ist der sogenannte Hauptbruchstrich, den man auf die Höhe des Gleichheitszeichens positionieren und den man auch länger als die anderen Bruchstriche ziehen sollte. Ein Unbeteiligter, der nicht die Entstehungsgeschichte der letzten Zeile kennt, würde die letzte Zeile also falsch interpretieren.
Geometrische Grundformen unbekannt
Werkzeuge wie Bohrer und Fräser können zylindrische oder keglige Schäfte aufweisen, um mit diesen das Werkzeug mit der Hauptspindel der Maschine zu verbinden. Eine Form der kegligen Schäfte ist der Morsekegel. Im Rahmen der Vorbesprechung einer Übung im Labor für Werkstoffbearbeitung zeigte sich, dass Studenten mit dem Begriff Morsekegel keine geometrische Vorstellung verbinden konnten.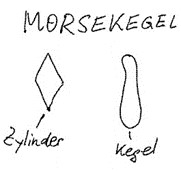 
Zur Klärung der Begriffe Zylinder und Kegel sollte ein Student die entsprechenden geometrischen Figuren an die Tafel zeichnen. Dabei entstand die Zeichnung aus Abbildung 8. Selbst die stark abstrahierte Darstellung lässt erkennen, dass dieser Student keine Vorstellung eines Zylinders hat und Kegel offensichtlich nur von der Bowlingbahn her kennt. Hier wurde zwar ein Einzelfall beschrieben, doch ist er symptomatisch für die starke Verringerung des Geometrieanteils in der Schulmathematik.
Schlussfolgerungen
Die präsentierten Beispiele zeigen deutlich, dass die Probleme der Studienanfängerinnen und Studienanfänger sich bereits bei sehr niedrigen Schwierigkeitsstufen ergeben und dass die Mathematikausbildung an Schulen bei Weitem nicht studienvorbereitend ist und selbst für den allgemeinbildenden Bereich nicht ausreicht.
Nach dem PISA-Schock im Jahr 2000 wurde der Mathematikunterricht an Schulen reformiert. Der Fokus lag nun mehr auf der Anwendung von Wissen. Die Vermittlung von Wissen selbst verlor an Bedeutung, das Üben wurde zu Gunsten von Anwendungen stark reduziert. Das Rechnen und auch das Umformen mathematischer Ausdrücke wurden an elektronische Hilfsmittel delegiert. In der Folge gab es noch weniger Anlässe, den elementaren Mittelstufenstoff zu üben. In der Bildungsdiskussion gibt es eine Unterschätzung des Übens und eine Unterschätzung von Kalkül. Dabei hat Kalkül einen Wert an sich, denn Kalkül hat oft algorithmische Aspekte, ist somit ein gutes Training für die Digitalisierung und in der Grundschule sicher sinnvoller als Programmieren. Es gibt eine Unterschätzung von Wissen. Doch Wissen ist wichtige Voraussetzung für Kreativität und für eine solide Internetrecherche. Dagegen werden der Taschenrechner und anwendungsbezogene Fragestellungen überschätzt.
Lehre sollte heute noch mehr als früher Wert auf Struktur legen. Denn die Struktur des Faches, die logische Einbettung und der rote Faden des Faches fördern das Verständnis. Die Studierenden neigen dazu, fallbasierend zu arbeiten. Sie suchen oft nach der Lösung genau dieses(!) einen Problems. Gegoogeltes Wissen ist aber unstrukturiert. Umso wichtiger wird in der Lehre die strukturelle Vernetzung von Wissen.
Dank
Wir danken unserem Kollegen Prof. Dr.-Ing. Ralf Förster, Beuth Hochschule für Technik Berlin, für die Beispiele und die vielen anregenden Diskussionen.
Referenzen
Affolter, Walter u. a. (2009). Das Mathematikbuch 9, Klett-Verlag, Ausgabe A ab 2009, ISBN 978-3-12-700391-8
Baumann (1017). Mathematikunterricht und Kompetenzorientierung – ein offener Brief . https://www.tagesspiegel.de/downloads/19549926/2/offener-brief.pdf (2018 10 12)
KMK. Abiturnoten im Ländervergleich. https://www.kmk.org/dokumentation-statistik/statistik/schulstatistik/abiturnoten.html (2018 10 12)
Sen BJW (2012). Die fünfte Prüfungskomponente im Abitur, Eine Handreichung, 3. überarbeitete Fassung, Hrsg Senatsverwaltung für Bildung, Jugend und Wissenschaft
Stellungnahme zu „Mathematikunterricht und Kompetenzorientierung – ein offener Brief“. https://www.tagesspiegel.de/downloads/19590132/1/mathematiker-distanzieren-sich-vom-mathematiker-brandbrief.pdf (2018 10 12)
Tgsp (1.7.2010). Der Tagesspiegel. https://www.tagesspiegel.de/berlin/schule/abschlussnoten-berliner-abiturienten-holen-bayerische-schueler-ein/1873312.html (2018 10 12)
Tgsp (22.3.2017). Der Tagesspiegel. „Mathematik häppchenweise“ , S. 22 https://www.tagesspiegel.de/wissen/brandbrief-gegen-bildungsstandards-der-aufstand-der-mathelehrer/19550928.html (2018 10 12)
Thoren, Katharina; Viole, Bianca; Harych, Peter; Brunner, Martin (2013). Abitur Berlin 2013 Ergebnisbericht, Institut für Schulqualität der Länder Berlin und Brandenburg e. V.
Vogt, Thomas (2017). Hausaufgaben für alle? In: Mitteilungen der Deutschen Mathematiker-Vereinigung, 25(2), p. 90-105
Quelle: Schwenk, Angela und Kalus, Norbert. KOMPETENZORIENTIERUNG IN DER DISKUSSION: BERLINER ABITUR-NOTEN, ELEMENTARMATHEMATISCHE FÄHIGKEITEN. In: Tagungsband der 13. Regionaltagung der Ingenieurpädagogischen Wissenschaftsgesellschaft, Hochschule Bochum 2018 – Diversität und Kulturelle Vielfalt – differenzieren, individualisieren – oder integrieren? In Druck.
Vorabveröffentlichung der Studie durch Schulforum-Berlin mit freundlicher Genehmigung der Autoren.
Studie als PDF-Datei: 2018_IPW-DFV_Schwenk_final
siehe auch: